Result
- Binary: 2
- Decimal: 10
- Hexadecimal: 16
Binary Calculator
Reviewed by
BS Román Ramos
An error occurred while performing the calculations. Please contact us through the form located on our contact page so we can fix it as soon as possible. Thank you very much.
Table of Contents
How to Use the Binary Calculator
Perform operations with binary numbers easily, quickly, and for free using our tool.
To do this, simply follow these steps:
- Enter the first binary number in the first box.
- Select the operation you wish to perform (addition, subtraction, multiplication, or division).
- Enter the second binary number.
- Press “Calculate”.
If you want to learn how to manually perform binary operations on your own, then continue reading this article.
What is the Binary Number System
The binary system, or binary numeral system, is a positional numeral system with base 2.
Unlike the decimal system (which has 10 as its base) the only digits that make up binary numbers are 0 and 1, which is why they are called binary numbers.
Among all numeral systems, this is, with the permission of the decimal system, the one you will find most often, because the basis of computing takes this system as a reference.
To indicate that a number has been written using the binary system, the subscript 2 is included, which indicates base 2 or binary:
$$ (0100)_{2} $$
Here, by introducing the number 2 as a base, we are indicating that it should be read: “zero one zero zero”, that is, the digits will be read individually and not interpreted as if it were the number “one hundred” in the decimal system.
How to Convert from Binary System to Decimal System
After having seen these preliminary indications, let's explain how we can transform a number written in base 2 to base 10 and vice versa.
To convert a binary number into a decimal one we must perform the procedure described in the following example:
$$(1101)_{2} \text{ to decimal}$$
Steps to follow:
- Place the digits of the binary number separated in a table, one digit per column.
- From right to left, place under each digit powers of 2, starting with the zero power (20).
- Perform the multiplication of each digit with the corresponding power.
- Finally, add up each of the results of the previous multiplications to obtain the decimal number.
The following table summarizes the procedure described above:
Steps | ||||||
1 | Binary number | 1 | 1 | 0 | 1 | |
2 | Powers of 2 | 23 | 22 | 21 | 20 | |
3 | Product: | (1)(23) | (1)(22) | (0)(21) | (1)(20) | |
4 | Sum | 8 | 4 | 0 | 1 | = 13 |
How to Convert from Decimal System to Binary System
To convert from the decimal system to a binary number, you must repeatedly divide the number by two, dividing, of course, the quotient of each operation, until the last result is the number 0.
$$N = (quotient)(2)+remainder$$
An example is provided below to more easily understand the procedure:
$$(75)_{10} \text{ to binary}$$
We start by dividing the number 76 by 2, which leaves us with a quotient of 36 and a remainder of 1.
Then we repeat the operation with the quotient repeatedly until it equals 0.
Here is the result of the process:
Decimal Number | Quotient | Remainder |
76 | 38 | 0 |
38 | 19 | 0 |
19 | 9 | 1 |
9 | 4 | 1 |
4 | 2 | 0 |
2 | 1 | 0 |
1 | 0 | 1 |
= 1001100 |
Therefore, we can conclude that the number 76 expressed in binary would be 1001100, read from top to bottom, meaning the remainder of the division of 1/2 is the first number we place from left to right when expressing the figure in binary code.
Operations with Binary Numbers
Binary Addition
Adding in binary can be done easily following this table:
$$ \begin{array}{|c|c|} \hline +& 0 & 1 \\\hline 0 & 0 & 1\\\hline 1 & 0 & 10\\\hline \end{array}$$
You can observe that 12+12=102, which is equivalent to 2 in the decimal system.
Here are more examples:
Example 1: 10112 + 0102
$$ \begin{array}{r} 1011 \\ + \,\,010\\ \hline 1011 \end{array}$$
Example 2: 1010112 + 1001112
$$ \begin{array}{r} 101011 \\ + 100110\\ \hline 1010001 \end{array}$$
Binary Subtraction
Subtraction is not commutative and therefore the elements involved in the operation must be distinguished: minuend and subtrahend. The minuend is the element from which the subtrahend is subtracted.
To perform binary subtraction, what is known as two's complement must be calculated.
To calculate the two's complement of a binary number, proceed as follows:
Consider the number N=41 as an example, whose binary representation is 41=1010012 where n=6 digits.
The two's complement of 41 is given by:
$$ 2^n-N = 2^6 – 41 = 23 =010111_{2} $$
In this way, to calculate the subtraction of binary numbers we must first calculate the two's complement of the subtrahend and then perform the addition. If there is a carry, it is disregarded.
Example 1: 0101112 – 0001102
The subtrahend 000110 is complemented to two.
$$ 000110 = 6 $$
$$ 2^6-6 = 58 = 0111010_2 $$
Now we perform the addition:
$$ \begin{array}{r} 010111 \\ + 111010\\ \hline 1010001 \end{array}$$
We disregard the carry bit, thus the subtraction finally is:
$$10001_{1}=17$$
Example 2: 0100112 – 1111002
We make the two's complement of 111100:
$$ 111100 = 60 $$
$$ 2^6 -60 = 4 = 000100_{2} $$
Now we perform the addition:
$$ \begin{array}{r} 010011 \\ + 000100\\ \hline 010111 \end{array}$$
In this way, we have that the result of the operation is 23.
Binary Multiplication
In multiplication, the elements are called multiplicand and multiplier. The elements involved in the operation are called factors.
The table for multiplying binaries is presented as follows:
$$ \begin{array}{|c|c|} \hline \times& 0 & 1 \\\hline 0 & 0 & 0\\\hline 1 & 0 & 1\\\hline \end{array}$$
Binary multiplication is carried out analogously to decimal multiplication. Let's see some examples here.
Example 1: 1012 x 112
$$ \begin{array}{r} 101 \\ \times \,\, 11\\\hline 101\\ 101\,\,\\\hline 1111 \end{array}$$
Example 2: 1101102x 1102
$$ \begin{array}{r} 110110\\ \times \,\, 110\\\hline 000000\\ 110110\,\,\\ 110110\quad \\\hline 101000100 \end{array}$$
Binary Division
Binary division follows the same principle as decimal division.
In the following example, the procedure you should follow is described step by step.
Example: 111012 / 102
We consider the first two digits of the dividend, and look for a multiple of the divisor that is close to 102. In this case, that value is 1.
We proceed in a manner similar to the previous step. The next digit (1), with which the new dividend is 112 and again the multiple of 102, close to 112 is the same value.
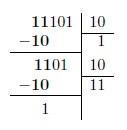
Finally, repeating the procedure we see that the result of the division is 11102, with a remainder of 1.
This has been all you need to know to perform operations with binary numbers, in this article we have presented how to perform the operations of addition, subtraction, multiplication, and division of binary numbers.
If you liked this article or the binary calculator do not forget to share it on your social networks, so that others can also learn.
We appreciate it if you find errors in our calculators, please let us know using the contact form so we can fix them as soon as possible.
