Kalkulator binarny

Jak używać kalkulatora binarnego

Wykonuj operacje na liczbach binarnych w łatwy, szybki i bezpłatny sposób, korzystając z naszego narzędzia.

Aby to zrobić, wystarczy wykonać następujące kroki:

1. W pierwszym polu wpisz pierwszą liczbę binarną.
2. Wybierz operację, którą chcesz wykonać (dodawanie, odejmowanie, mnożenie lub dzielenie).
3. Wprowadź drugą liczbę binarną.
4. Naciśnij „Oblicz”.

Jeśli chcesz nauczyć się samodzielnie wykonywać operacje na liczbach binarnych ręcznie, kontynuuj czytanie tego artykułu.

Co to jest system liczbowy binarny

System binarny, czyli system liczbowy binarny, to system liczbowy pozycyjny o podstawie 2.

W przeciwieństwie do systemu dziesiętnego (który ma podstawę 10) jedynymi cyframi tworzącymi liczby binarne są 0 i 1, dlatego nazywane są liczbami binarnymi.

Spośród wszystkich systemów liczbowych, ten jest, obok systemu dziesiętnego, najczęściej spotykany, ponieważ stanowi podstawę informatyki.

Aby wskazać, że liczba została zapisana za pomocą systemu binarnego, dodaje się indeks dolny 2, który oznacza podstawę 2 lub binarną:

$$ (0100)_{2} $$

Tutaj, wprowadzając liczbę 2 jako podstawę, wskazujemy, że należy ją czytać: „ zero jeden zero zero” , czyli cyfry będą czytane indywidualnie, a nie interpretowane jako liczba „ sto” w systemie dziesiętnym.

Jak przekształcić system binarny na system dziesiętny

Po zapoznaniu się z tymi wstępnymi wskazówkami, wyjaśnimy, jak możemy przekształcić liczbę zapisaną w systemie o podstawie 2 na system o podstawie 10 i odwrotnie.

Aby przekształcićliczbę binarną na dziesiętną , musimy wykonać procedurę opisaną na poniższym przykładzie:

$$(1101)_{2} \text{ na dziesiętny}$$

Kolejne kroki:

1. Umieszczamy cyfry liczby binarnej oddzielone w tabeli, jedna cyfra na kolumnę.
2. Od prawej do lewej pod każdą cyfrą umieszczamy potęgi liczby 2, zaczynając od potęgi zerowej (2 ⁰ ).
3. Wykonujemy mnożenie każdej cyfry przez odpowiadającą jej potęgę.
4. Ostatecznie sumujemy wszystkie wyniki poprzednich mnożeń, aby uzyskać liczbę dziesiętną.

Poniższa tabela podsumowuje opisaną procedurę:

Jak przekształcić system dziesiętny na system binarny

Aby przekształcić system dziesiętny na liczbę binarną, należy dzielić daną liczbę kolejno przez dwa, dzieląc za każdym razem iloraz z każdej operacji, aż ostatni wynik będzie równy 0.

$$N = (iloraz)(2)+reszta$$

Poniżej znajduje się przykład, który pomoże łatwiej zrozumieć procedurę:

$$(75)_{10} \text{ na binarny}$$

Zaczynamy od podzielenia liczby 76 przez 2, co daje nam iloraz 36 i resztę 1.

Następnie powtarzamy operację z ilorazem wielokrotnie, aż będzie równy 0.

Oto wynik procesu:

W związku z tym możemy stwierdzić, że liczba 76 wyrażona w systemie binarnym to 100110 0 , czytane od góry do dołu, czyli reszta z dzielenia 1/2 jest pierwszą liczbą, którą umieszczamy od lewej do prawej, wyrażając liczbę w kodzie binarnym.

Operacje na liczbach binarnych

Dodawanie binarne

Dodawanie w systemie binarnym możemy łatwo wykonać, korzystając z poniższej tabeli:

$$ \begin{array}{|c|c|} \hline +& 0 & 1 \\\hline 0 & 0 & 1\\\hline 1 & 0 & 10\\\hline \end{array}$$

Możesz zauważyć, że 1 ₂ +1 ₂ =10 ₂ , co jest równoważne 2 w systemie dziesiętnym.

Oto więcej przykładów:

Przykład 1: 1011 ₂ + 010 ₂

$$ \begin{array}{r} 1011 \\ + \,\,010\\ \hline 1011 \end{array}$$

Przykład 2: 101011 ₂ + 100111 ₂

$$ \begin{array}{r} 101011 \\ + 100110\\ \hline 1010001 \end{array}$$

Odejmowanie binarne

Odejmowanie nie jest przemienne, dlatego należy rozróżnić elementy biorące udział w operacji: odjemną i odjemnik. Odjemna to element, od którego odejmujemy odjemnik.

Aby wykonać odejmowanie binarne, należy wykonać to, co jest znane jako dopełnienie dodwóch.

Aby obliczyć dopełnienie do dwóch liczby binarnej, postępujemy w następujący sposób:

Rozważmy liczbę N=41 jako przykład, której reprezentacja binarna to 41=101001 ₂ gdzie n=6 cyfr.

Dopełnienie do dwóch liczby 41 wynosi:

$$ 2^n-N = 2^6 – 41 = 23 =010111_{2} $$

W ten sposób, aby obliczyć odejmowanie liczb binarnych, musimy najpierw obliczyć dopełnienie do dwóch odjemnika, a następnie wykonujemy dodawanie. Jeśli występuje przeniesienie, jest ono ignorowane.

Przykład 1: 010111 ₂ – 000110 ₂

Odjemnik 000110 jest dopełniany do dwóch.

$$ 000110 = 6 $$

$$ 2^6-6 = 58 = 0111010_2 $$

Teraz wykonujemy dodawanie:

$$ \begin{array}{r} 010111 \\ + 111010\\ \hline 1010001 \end{array}$$

Ignorujemy bit przeniesienia, w ten sposób kończąc odejmowanie:

$$10001_{1}=17$$

Przykład 2: 010011 ₂ – 111100 ₂

Wykonujemy dopełnienie do dwóch 111100:

$$ 111100 = 60 $$

$$ 2^6 -60 = 4 = 000100_{2} $$

Teraz wykonujemy dodawanie:

$$ \begin{array}{r} 010011 \\ + 000100\\ \hline 010111 \end{array}$$

W ten sposób wynik operacji to 23.

Mnożenie binarne

W mnożeniu elementy nazywane są mnożną i mnożnikiem. Elementy biorące udział w operacji nazywane są czynnikami.

Tabela do mnożenia binarnego przedstawia się następująco:

$$ \begin{array}{|c|c|} \hline \times& 0 & 1 \\\hline 0 & 0 & 0\\\hline 1 & 0 & 1\\\hline \end{array}$$

Mnożenie binarne wykonuje się w sposób analogiczny do mnożenia dziesiętnego. Oto kilka przykładów.

Przykład1: 101₂x 11₂

$$ \begin{array}{r} 101 \\ \times \,\, 11\\\hline 101\\ 101\,\,\\\hline 1111 \end{array}$$

Przykład 2: 110110 ₂ x 110 ₂

$$ \begin{array}{r} 110110\\ \times \,\, 110\\\hline 000000\\ 110110\,\,\\ 110110\quad \\\hline 101000100 \end{array}$$

Dzielenie binarne

Dzielenie w systemie binarnym opiera się na tych samych zasadach co dzielenie dziesiętne.

W poniższym przykładzie opisano krok po kroku procedurę, którą należy wykonać.

Przykład: 11101 ₂ / 10 ₂

Rozważamy pierwsze dwa cyfry dzielnej i szukamy wielokrotności dzielnika, która jest najbliższa 102. W tym przypadku ta wartość to 1.

Postępujemy dzielnik to 112, a najbliższy wielokrotność 102 do 112 to ta sama wartość.

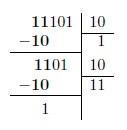
Ostatecznie, powtarzając procedurę, widzimy, że wynik dzielenia to 11102, z resztą 1.

To wszystko, co musisz wiedzieć, aby wykonywać operacje na liczbach binarnych. W tym artykule przedstawiliśmy, jak przeprowadzać operacje dodawania, odejmowania, mnożenia i dzielenia liczbbinarnych.

Jeśli ten artykuł lub kalkulator binarny przypadły Ci do gustu, nie zapomnij podzielić się nim w swoich sieciach społecznościowych, aby inni również mogli się nauczyć.

Dziękujemy za zgłaszanie błędów w naszych kalkulatorach za pomocą formularza kontaktowego, abyśmy mogli jak najszybciej je naprawić.

Lic. Román Ramos

Magister matematyki i magister badań operacyjnych na UCV.

Román Ramos jest licencjatem matematyki na Centralnym Uniwersytecie Wenezueli (UCV) ... Czytaj więcej »