Calculadora hexadecimal

Como usar a calculadora hexadecimal

Você pode realizar operações com números hexadecimais de forma fácil usando nossa ferramenta. Para isso, basta fazer o seguinte:

1. Coloque na primeira caixa o primeiro número hexadecimal.
2. Selecione a operação que deseja realizar (soma, subtração, multiplicação ou divisão).
3. Insira o segundo número em hexadecimal.
4. Finalmente, pressione “Calcular”.

Se você deseja aprender a realizar manualmente as operações em hexadecimal, continue lendo este artigo.

Como converter hexadecimal para decimal e vice-versa

O sistema hexadecimal é um sistema de numeração posicional cuja base é o número 16.

Para expressar cada dígito, são usados até 16 símbolos distintos. Esses símbolos são formados pelos dígitos tradicionais do sistema decimal (0 a 9) e as seis primeiras letras do alfabeto (A, B, C, D, E, F).

Para realizar a conversão, é conveniente usar a seguinte tabela hexadecimal:

Operações com números hexadecimais

Incremento

Quando se incrementa em hexadecimal, cada posição dos dígitos é incrementada uma unidade de 0 até F. Quando o dígito é F e se soma uma unidade, o resultado é um zero e se incrementa o dígito da posição seguinte.

Exemplo de sequência que começa em 29:

29, 2A, 2B, 2C, 2D, 2E, 2F, 30, 31...

Exemplo de sequência que começa em 5FB:

5FB, 5F9, 5FA, 5FB, 5FC, 5FD, 5FE, 5FF, 600, 601...

Soma hexadecimal

A soma hexadecimal segue as mesmas regras da soma decimal, considerando que o dígito de maior valor é o F.

Você pode seguir este procedimento:

1. Somar os dois dígitos hexadecimais em decimal, inserindo o equivalente hexadecimal para números maiores que 9
2. Se a soma é igual ou menor a 15 , esta pode ser expressa como dígito hexadecimal.
3. Se a soma é maior ou igual a 16 , subtrai-se 16 e se carrega um (1) para o dígito da próxima posição.

Exemplo 1: 28 ₁₆ + 54 ₁₆

$$ \begin{array}{r}

Exemplo 1: 28 ₁₆ + 54 ₁₆

$$ \begin{array}{r} 28 \\ + \,\, 54\\ \hline 7C \end{array}$$

Exemplo 2: B7 ₁₆ + 26 ₁₆

$$ \begin{array}{r} B7 \\ + \,\, 26\\\hline DD \end{array}$$

Exemplo 3: 1FE ₁₆ + 95A ₁₆

$$ \begin{array}{r} 1FE \\ + \,\, 95A\\\hline B58 \end{array}$$

Subtração hexadecimal

Para subtrair números hexadecimais, utiliza-se o mesmo método que para a subtração binária. Ou seja, em vez de subtrair, soma-se o complemento a 2 do número hexadecimal.

O subtraendo hexadecimal é complementado a 2 e depois somado ao minuendo. Se houver carry, ele é ignorado.

Exemplo 1: 5CA ₁₆ – 42C ₁₆

O subtraendo 42C é complementado a 2 da seguinte forma:

Então, realiza-se a soma:

$$ \begin{array}{r} 5CA \\ + \,\, BD4\\\hline 119E \end{array}$$

Ignora-se o bit de carry e a subtração resulta em 19E.

Exemplo 2: 7F4B ₁₆ – 3ABC ₁₆

Fazemos o complemento a 2 de 3ABC:

Realiza-se a soma:

$$ \begin{array}{r} 7F4B \\ + \,\, D654\\\hline 1459F \end{array}$$

Ignora-se o bit de carry e a subtração resulta em 459F.

Multiplicação hexadecimal

Para realizar a multiplicação, é importante usar a seguinte tabela de multiplicação hexadecimal, similar à usada no caso decimal.

O que se deseja é realizar a multiplicação hexadecimal de forma análoga à multiplicação decimal.

Exemplo 1: F610 ₁₆ x BE ₁₆

$$ \begin{array}{r} F610 \\ \times \,\, BE\\\hline D74E0\\ A92B0\quad \\\hline B69FE0 \end{array}$$

Exemplo 2: 47A1 ₁₆ x DB ₁₆

$$ \begin{array}{r} 47A1 \\ \times \,\, DB\\\hline 313EB\\ 3A32D \quad \\\hline 3D46BB \end{array}$$

Divisão hexadecimal

A divisão hexadecimal segue o mesmo princípio que em outros sistemas numéricos. Vejamos um exemplo onde realizaremos a divisão passo a passo.

Exemplo: AE887 ₁₆ / 3A ₁₆

O primeiro passo será realizar uma tabela com os múltiplos de 3A, que são:

Buscamos na tabela o primeiro múltiplo de 3A próximo aos dois primeiros dígitos (AE). Neste caso, é 3.

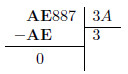
Procedemos de maneira análoga ao passo anterior. O dígito seguinte (8) é menor que 3A, razão pela qual adicionamos um zero ao quociente e realizamos a divisão ao 88.

Buscamos um múltiplo de 3A próximo a 88. Revisando na tabela, apreciamos que este valor é 2, cujo múltiplo é 74.

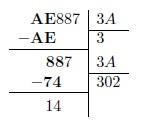
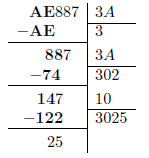
Finalmente, repetindo o procedimento, vemos que o resultado da divisão é 3025, ficando como resto 25.

Isso foi tudo o que você precisa saber para realizar operações com números hexadecimais, neste artigo você aprendeu passo a passo como efetuar a soma, subtração, multiplicação e divisão de número em hexadecimal.

Se você está satisfeito(a) com o artigo ou com o calculador hexadecimal online, não deixe de compartilhá-los em suas redes sociais, para que outras pessoas também desfrutem desta comunidade.

Bach. Román Ramos

Licenciado em Matemática e Mestre em Pesquisa Operacional pela UCV.

Román Ramos é Licenciado em Matemática pela Universidade Central da Venezuela (UCV) e ... Ler mais »