Binärrechner

Wie man den Binärrechner benutzt

Führen Sie Operationen mit Binärzahlen auf einfache, schnelle und kostenlose Weise mit unserem Tool durch.

Dazu müssen Sie nur Folgendes tun:

1. Geben Sie in das erste Feld die erste Binärzahl ein.
2. Wählen Sie die Operation aus, die Sie durchführen möchten (Addition, Subtraktion, Multiplikation oder Division).
3. Geben Sie die zweite Binärzahl ein.
4. Drücken Sie „Berechnen“.

Wenn Sie lernen möchten, wie Sie Binäroperationen manuell durchführen, lesen Sie bitte weiter in diesem Artikel.

Was ist das Binärzahlensystem

Das Binärsystem, oder binäres Zahlensystem, ist ein positionales Zahlensystem mit der Basis 2.

Im Gegensatz zum Dezimalsystem (das die Basis 10 hat), bestehen die Zahlen im Binärsystem nur aus den Ziffern 0 und 1, weshalb sie als Binärzahlen bezeichnet werden.

Unter allen Zahlensystemen ist dieses, mit Erlaubnis des Dezimalsystems, dasjenige, das Sie am häufigsten finden werden, da die Informatik dieses System als Referenz nimmt.

Um anzugeben, dass eine Zahl im Binärsystem geschrieben wurde, wird der Index 2 hinzugefügt, der Basis 2 oder binär bedeutet:

$$ (0100)_{2} $$

Hier, indem wir die Zahl 2 als Basis einführen, signalisieren wir, dass es als „ null eins null null“ gelesen werden soll, das heißt, die Ziffern werden einzeln gelesen und nicht als die Zahl „ hundert“ im Dezimalsystem interpretiert.

Wie man vom Binärsystem ins Dezimalsystem umwandelt

Nachdem wir diese kleinen vorläufigen Hinweise gesehen haben, werden wir erklären, wie wir eine Zahl, die mit Basis 2 geschrieben wurde, in Basis 10 umwandeln können und umgekehrt.

Um eine Binärzahl in eine Dezimalzahl umzuwandeln , müssen wir das Verfahren durchführen, das im Folgenden beispielhaft beschrieben wird:

$$(1101)_{2} \text{ in Dezimal}$$

Schritte, die durchgeführt werden müssen:

1. Wir platzieren die Ziffern der Binärzahl in einer Tabelle, eine Ziffer pro Spalte.
2. Von rechts nach links platzieren wir unter jeder Ziffer Potenzen von 2, beginnend mit der Potenz Null (2 ⁰ ).
3. Wir führen die Multiplikation jeder Ziffer mit der entsprechenden Potenz durch.
4. Schließlich addieren wir jedes der Ergebnisse der vorherigen Multiplikationen, um so die Dezimalzahl zu erhalten.

Die folgende Tabelle fasst das beschriebene Verfahren zusammen:

Wie man vom Dezimalsystem ins Binärsystem umwandelt

Um vom Dezimalsystem in eine Binärzahl zu wechseln, müssen Sie die betreffende Zahl wiederholt durch zwei teilen, wobei jedes Mal der Quotient der Operation geteilt wird, bis das letzte Ergebnis die Zahl 0 ist.

$$N = (Quotient)(2)+Rest$$

Im Folgenden wird ein Beispiel durchgeführt, um das Verfahren leichter zu verstehen:

$$(75)_{10} \text{ in Binär}$$

Wir beginnen mit der Teilung der Zahl 76 durch 2, was uns einen Quotienten von 36 und einen Rest von 1 hinterlässt.

Dann wiederholen wir die Operation mit dem Quotienten wiederholt, bis dieser gleich 0 ist.

Hier haben Sie das Ergebnis des Prozesses:

Daher können wir schlussfolgern, dass die Zahl 76 in Binär 100110 0 ausgedrückt wird, sie wird von oben nach unten gelesen, das heißt, der Rest der Teilung von 1/2 ist die erste Zahl, die wir von links nach rechts platzieren, wenn wir die Ziffer in Binärcode ausdrücken.

Operationen mit Binärzahlen

Binäre Addition

Addieren in Binär können wir leicht anhand der folgenden Tabelle durchführen:

$$ \begin{array}{|c|c|} \hline +& 0 & 1 \\\hline 0 & 0 & 1\\\hline 1 & 0 & 10\\\hline \end{array}$$

Sie können sehen, dass 1 ₂ +1 ₂ =10 ₂ , was dem Äquivalent von 2 im Dezimalsystem entspricht.

Hier haben Sie weitere Beispiele:

Beispiel 1: 1011 ₂ + 010 ₂

$$ \begin{array}{r} 1011 \\ + \,\,010\\ \hline 1011 \end{array}$$

Beispiel 2: 101011 ₂ + 100111 ₂

$$ \begin{array}{r} 101011 \\ + 100110\\ \hline 1010001 \end{array}$$

Binäre Subtraktion

Die Subtraktion ist nicht kommutativ und daher müssen die Elemente, die an der Operation beteiligt sind, unterschieden werden: Minuend und Subtrahend. Der Minuend ist das Element, von dem der Subtrahend abgezogen wird.

Um die binäre Subtraktion durchzuführen, muss das, was als Zweierkomplement bekannt ist, berechnet werden.

Um das Zweierkomplement einer Binärzahl zu berechnen, gehen wir wie folgt vor:

Betrachten wir die Zahl N=41 als Beispiel, deren binäre Darstellung 41=101001 ₂ mit n=6 Ziffern ist.

Das Zweierkomplement von 41 ist gegeben durch:

$$ 2^n-N = 2^6 – 41 = 23 =010111_{2} $$

Auf diese Weise müssen wir, um die Subtraktion von Binärzahlen zu berechnen, zuerst das Zweierkomplement des Subtrahenden berechnen und dann die Addition durchführen. Wenn es einen Übertrag gibt, wird dieser ignoriert.

Beispiel 1: 010111 ₂ – 000110 ₂

Der Subtrahend 000110 wird zum Zweierkomplement ergänzt.

$$ 000110 = 6 $$

$$ 2^6-6 = 58 = 0111010_2 $$

Nun führen wir die Addition durch:

$$ \begin{array}{r} 010111 \\ + 111010\\ \hline 1010001 \end{array}$$

Wir ignorieren den Übertrag, sodass die Subtraktion schließlich so aussieht:

$$10001_{1}=17$$

Beispiel 2: 010011 ₂ – 111100 ₂

Wir ergänzen 111100 zum Zweierkomplement:

$$ 111100 = 60 $$

$$ 2^6 -60 = 4 = 000100_{2} $$

Nun führen wir die Addition durch:

$$ \begin{array}{r} 010011 \\ + 000100\\ \hline 010111 \end{array}$$

Auf diese Weise haben wir das Ergebnis der Operation als 23.

Binäre Multiplikation

Bei der Multiplikation werden die Elemente Multiplikand und Multiplikator genannt. Die Elemente, die an der Operation beteiligt sind, heißen Faktoren.

Die Tabelle für die Multiplikation von Binärzahlen wird wie folgt dargestellt:

$$ \begin{array}{|c|c|} \hline \times& 0 & 1 \\\hline 0 & 0 & 0\\\hline 1 & 0 & 1\\\hline \end{array}$$

Die Multiplikation in Binär wird analog zur Dezimalmultiplikation durchgeführt. Hier sind einige Beispiele.

Beispiel1: 101₂x 11₂

$$ \begin{array}{r} 101 \\ \times \,\, 11\\\hline 101\\ 101\,\,\\\hline 1111 \end{array}$$

Beispiel 2: 110110 ₂ x 110 ₂

$$ \begin{array}{r} 110110\\ \times \,\, 110\\\hline 000000\\ 110110\,\,\\ 110110\quad \\\hline 101000100 \end{array}$$

Binäre Division

Die Division in Binär folgt demselben Prinzip wie die Division in Dezimal.

Im folgenden Beispiel wird Schritt für Schritt das Verfahren beschrieben, das Sie befolgen müssen.

Beispiel: 11101 ₂ / 10 ₂

Wir betrachten die ersten zwei Ziffern des Dividenden und suchen ein Vielfaches des Divisors, das nahe bei 102 liegt. In diesem Fall ist dieser Wert 1.

Wir fahren analog zum vorherigen Schritt fort. Die nächste Ziffer (1), damit der neue Der Dividend ist 112 und erneut ist das Vielfache von 102, das nächste zu 112, derselbe Wert.

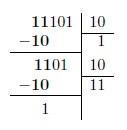
Schließlich sehen wir, dass das Ergebnis der Division 11102 ist, mit einem Rest von 1.

Das war alles, was du wissen musst, um Operationen mit Binärzahlen durchzuführen. In diesem Artikel haben wir dir gezeigt, wie man die Operationen der Addition, Subtraktion, Multiplikation und Division von Binärzahlen durchführt.

Wenn dir dieser Artikel oder der Binärrechner gefallen hat, zögere nicht, ihn in deinen sozialen Netzwerken zu teilen, damit auch andere Personen lernen können.

Wir danken dir, wenn du Fehler in unseren Rechnern findest und uns dies über das Kontaktformular mitteilst, damit wir sie so schnell wie möglich beheben können.

B.Sc. Román Ramos

Diplom in Mathematik und Master in Operations Research von der UCV.

Román Ramos hat einen Abschluss in Mathematik von der Universidad Central de Venezuela ... Mehr lesen »