Comment utiliser la calculatrice binaire

Effectuez des opérations avec des nombres binaires facilement, rapidement et gratuitement en utilisant notre outil.

Pour cela, suivez simplement les étapes suivantes :

1. Placez le premier nombre binaire dans la première case.
2. Sélectionnez l'opération que vous souhaitez effectuer (addition, soustraction, multiplication ou division).
3. Introduisez le second nombre en binaire.
4. Appuyez sur “Calculer”.

Si vous souhaitez apprendre à effectuer vous-même les opérations en binaire manuellement, continuez à lire cet article.

Qu'est-ce que le système de numération binaire

Le système binaire, ou système numérique binaire, est un système de numération positionnel avec base 2.

Contrairement au système décimal (qui a 10 comme base) les seuls chiffres qui composent les nombres binaires sont 0 et 1, c'est pourquoi ils sont appelés nombres binaires.

Parmi tous les systèmes de numération, celui-ci est, avec la permission du système décimal, celui que vous trouverez le plus souvent, car la base de l'informatique prend ce système comme référence.

Pour indiquer qu'un nombre a été écrit en utilisant le système binaire, on inclut le sous-indice 2, qui indique la base 2 ou binaire :

$$ (0100)_{2} $$

Ici, en introduisant le nombre 2 comme base, nous indiquons qu'il doit être lu : “ zéro un zéro zéro” , c'est-à-dire, les chiffres seront lus individuellement et non interprétés comme s'il s'agissait du nombre “ cent” dans le système décimal.

Comment convertir du système binaire au système décimal

Après avoir vu ces petites indications préliminaires, nous allons expliquer comment nous pouvons transformer un nombre écrit en base 2 en base 10 et vice versa.

Pour convertir un nombre binaire en un nombre décimal , nous devons effectuer la procédure décrite de manière exemplaire ci-dessous :

$$(1101)_{2} \text{ en décimal}$$

Étapes à suivre :

1. Nous plaçons les chiffres du nombre binaire séparés dans un tableau, un chiffre par colonne.
2. De droite à gauche, nous plaçons sous chaque chiffre des puissances de 2, en commençant par la puissance zéro (2 ⁰ ).
3. Nous effectuons la multiplication de chaque chiffre avec la puissance correspondante.
4. Finalement, nous additionnons chacun des résultats des multiplications précédentes pour ainsi obtenir le nombre décimal.

Le tableau suivant résume la procédure décrite ci-dessus :

Comment convertir du système décimal au système binaire

Pour passer du système décimal à un nombre binaire, vous devez diviser ce nombre successivement par deux, en divisant, bien sûr, le quotient de chaque opération, jusqu'à ce que le dernier résultat soit le nombre 0.

$$N = (quotient)(2)+reste$$

Voici un exemple pour comprendre plus facilement la procédure :

$$(75)_{10} \text{ en binaire}$$

Nous commençons par diviser le nombre 76 par 2, ce qui nous donne un quotient de 36 et un reste de 1.

Ensuite, nous répétons l'opération avec le quotient de manière répétée jusqu'à ce qu'il soit égal à 0.

Voici le résultat du processus :

Par conséquent, nous pouvons conclure que le nombre 76 exprimé en binaire serait 100110 0 , ils se lisent de haut en bas, c'est-à-dire que le reste de la division de 1/2 est le premier nombre que nous placerons de gauche à droite en exprimant le chiffre en code binaire.

Opérations avec des nombres binaires

Addition binaire

Ajouter en binaire peut être fait facilement en suivant le tableau suivant :

$$ \begin{array}{|c|c|} \hline +& 0 & 1 \\\hline 0 & 0 & 1\\\hline 1 & 0 & 10\\\hline \end{array}$$

Vous pouvez observer que 1 ₂ +1 ₂ =10 ₂ , ce qui équivaut à 2 dans le système décimal.

Voici plus d'exemples :

Exemple 1: 1011 ₂ + 010 ₂

$$ \begin{array}{r} 1011 \\ + \,\,010\\ \hline 1011 \end{array}$$

Exemple 2: 101011 ₂ + 100111 ₂

$$ \begin{array}{r} 101011 \\ + 100110\\ \hline 1010001 \end{array}$$

Soustraction binaire

La soustraction n'est pas commutative et par conséquent, il faut distinguer les éléments qui interviennent dans l'opération : le minuend et le soustraire. Le minuend est l'élément duquel on soustrait le soustraire.

Pour effectuer la soustraction binaire, il faut réaliser ce que l'on connaît comme complément à deux .

Pour calculer le complément à deux d'un nombre binaire, on procède de la manière suivante :

Considérons le nombre N=41 comme exemple, dont la représentation binaire est 41=101001 ₂ où n=6 chiffres.

Le complément à deux de 41 est donné par :

$$ 2^n-N = 2^6 – 41 = 23 =010111_{2} $$

De cette manière, pour calculer la soustraction de nombres binaires, nous devons d'abord calculer le complément à deux du soustraire, puis effectuer l'addition. Si un report existe, il est ignoré.

Exemple 1: 010111 ₂ – 000110 ₂

Le soustraire 000110 est complété à deux.

$$ 000110 = 6 $$

$$ 2^6-6 = 58 = 0111010_2 $$

Maintenant, nous effectuons l'addition :

$$ \begin{array}{r} 010111 \\ + 111010\\ \hline 1010001 \end{array}$$

Nous ignorons le bit de report, ce qui donne finalement la soustraction comme ceci :

$$10001_{1}=17$$

Exemple 2: 010011 ₂ – 111100 ₂

Nous faisons le complément à 2 de 111100 :

$$ 111100 = 60 $$

$$ 2^6 -60 = 4 = 000100_{2} $$

Maintenant, nous effectuons l'addition :

$$ \begin{array}{r} 010011 \\ + 000100\\ \hline 010111 \end{array}$$

Ainsi, nous avons que le résultat de l'opération est 23.

Multiplication binaire

Dans la multiplication, les éléments s'appellent multiplicande et multiplicateur. Les éléments qui interviennent dans l'opération sont appelés facteurs.

Le tableau pour multiplier en binaire se présente ainsi :

$$ \begin{array}{|c|c|} \hline \times& 0 & 1 \\\hline 0 & 0 & 0\\\hline 1 & 0 & 1\\\hline \end{array}$$

La multiplication en binaire s'effectue de manière analogue à la multiplication décimale. Voici ici quelques exemples.

Exemple 1: 101 ₂ x 11 ₂

$$ \begin{array}{r} 101 \\ \times \,\, 11\\\hline 101\\ 101\,\,\\\hline 1111 \end{array}$$

Exemple 2: 110110 ₂ x 110 ₂

$$ \begin{array}{r} 110110\\ \times \,\, 110\\\hline 000000\\ 110110\,\,\\ 110110\quad \\\hline 101000100 \end{array}$$

Division binaire

La division en binaire suit le même principe que la division décimale.

Dans l'exemple suivant, la procédure à suivre est décrite étape par étape.

Exemple: 11101 ₂ / 10 ₂

Nous considérons les deux premiers chiffres du dividende, et nous cherchons un multiple du diviseur qui soit proche de 102. Dans ce cas, cette valeur est 1.

Nous procédons de manière analogue à l'étape précédente. Le chiffre suivant (1), avec lequel le nouveau Le dividende est 112 et à nouveau le multiple de 102, le plus proche de 112 est la même valeur.

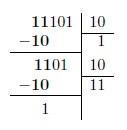
Finalement, en répétant la procédure, nous voyons que le résultat de la division est 11102, avec un reste de 1.

Cela a été tout ce que vous devez savoir pour effectuer des opérations avec des nombres binaires, dans cet article nous vous avons présenté comment réaliser les opérations de addition, soustraction, multiplication et division de nombres binaires .

Si cet article ou la calculatrice binaire vous ont plu, n'hésitez pas à le partager sur vos réseaux sociaux, afin que d'autres personnes puissent également apprendre.

Nous vous remercions de nous signaler toute erreur dans nos calculatrices, en utilisant le formulaire de contact pour que nous puissions les corriger dès que possible.