Como usar a calculadora binária

Realize operações com números binários de forma fácil, rápida e gratuita usando nossa ferramenta.

Para isso, basta fazer o seguinte:

1. Coloque na primeira caixa o primeiro número binário.
2. Selecione a operação que deseja realizar (soma, subtração, multiplicação ou divisão).
3. Introduza o segundo número em binário.
4. Pressione “Calcular”.

Se você deseja aprender a realizar por conta própria as operações em binário de forma manual, então continue lendo este artigo.

O que é o sistema de numeração binário

O sistema binário, ou sistema numérico binário, é um sistema de numeração posicional com base 2.

Ao contrário do sistema decimal (que tem 10 como base) as únicas cifras que compõem os números binários são 0 e 1, é por isso que são chamados de números binários.

Entre todos os sistemas de numeração, este é, com a permissão do sistema decimal, o que você encontrará mais vezes, porque a base da informática toma este sistema como referência.

Para indicar que um número foi escrito através do sistema binário inclui-se o subscrito 2, que indica base 2 ou binária:

$$ (0100)_{2} $$

Aqui, ao introduzir o número 2 como base, estamos sinalizando que deve ser lido: “zero um zero zero”, ou seja, as cifras serão lidas individualmente e não será interpretado como se fosse o número “cem” do sistema decimal.

Como converter do sistema binário para o sistema decimal

Após ter visto essas pequenas indicações preliminares, vamos explicar como podemos transformar um número escrito com base 2 para base 10 e vice-versa.

Para converter um número binário em um decimal devemos realizar o procedimento que se descreve de forma exemplificada a seguir:

$$(1101)_{2} \text{ para decimal}$$

Passos a realizar:

1. Colocamos os dígitos do número binário separados em uma tabela, um dígito por coluna.
2. Da direita para a esquerda coloca-se abaixo de cada dígito potências de 2, começando com a potência zero (2⁰).
3. Realizamos a multiplicação de cada dígito com a potência correspondente.
4. Finalmente soma-se cada um dos resultados das multiplicações anteriores para assim obter o número decimal.

A tabela a seguir resume o procedimento descrito anteriormente:

Como converter do sistema decimal para o sistema binário

Para passar do sistema decimal para um número binário, você deve dividir esse número sucessivas vezes por dois, dividindo, é claro, o quociente de cada operação, até que o último resultado seja o número 0.

$$N = (quociente)(2)+resto$$

A seguir, será realizado um exemplo para entender mais facilmente o procedimento:

$$(75)_{10} \text{ para binário}$$

Começamos realizando a divisão do número 76 por 2, o que nos deixa com quociente 36 e resto 1.

Depois repetimos a operação com o quociente de forma reiterada até que este seja igual a 0.

Aqui você tem o resultado do processo:

Portanto, podemos concluir que o número 76 expresso em binário seria 1001100, lidos de cima para baixo, ou seja, o resto da divisão de 1/2, é o primeiro número que colocaremos da esquerda para a direita ao expressar a cifra em código binário.

Operações com números binários

Soma binária

Somar em binário podemos fazer facilmente seguindo a seguinte tabela:

$$ \begin{array}{|c|c|} \hline +& 0 & 1 \\\hline 0 & 0 & 1\\\hline 1 & 0 & 10\\\hline \end{array}$$

Você pode observar que 1₂+1₂=10₂, que é o equivalente a 2 no sistema decimal.

Aqui você tem mais exemplos:

Exemplo 1: 1011₂ + 010₂

$$ \begin{array}{r} 1011 \\ + \,\,010\\ \hline 1011 \end{array}$$

Exemplo 2: 101011₂ + 100111₂

$$ \begin{array}{r} 101011 \\ + 100110\\ \hline 1010001 \end{array}$$

Subtração binária

A subtração não é comutativa e, portanto, devem ser distinguidos os elementos que intervêm na operação: minuendo e subtraendo. O minuendo é o elemento do qual se subtrai o subtraendo.

Para realizar a subtração binária deve-se realizar o que se conhece como complemento a dois.

Para calcular o complemento a dois de um número binário procede-se da seguinte maneira:

Consideremos o número N=41 como exemplo, cuja representação binária é 41=101001₂ onde n=6 dígitos.

O complemento a dois de 41 é dado por:

$$ 2^n-N = 2^6 – 41 = 23 =010111_{2} $$

Dessa forma, para calcular a subtração de números binários devemos primeiro calcular o complemento a dois do subtraendo e depois efetua-se a soma. Se existir transporte, ele é desprezado.

Exemplo 1: 010111₂ – 000110₂

O subtraendo 000110 é complementado a dois.

$$ 000110 = 6 $$

$$ 2^6-6 = 58 = 0111010_2 $$

Agora efetuamos a soma:

$$ \begin{array}{r} 010111 \\ + 111010\\ \hline 1010001 \end{array}$$

Desprezamos o bit de transporte ficando assim a subtração finalmente assim:

$$10001_{1}=17$$

Exemplo 2: 010011₂ – 111100₂

Fazemos o complemento a 2 de 111100:

$$ 111100 = 60 $$

$$ 2^6 -60 = 4 = 000100_{2} $$

Agora efetuamos a soma:

$$ \begin{array}{r} 010011 \\ + 000100\\ \hline 010111 \end{array}$$

Dessa maneira temos que o resultado da operação é 23.

Multiplicação binária

Na multiplicação os elementos se chamam multiplicando e multiplicador. Os elementos que intervêm na operação se chamam fatores.

A tabela para multiplicar binários se apresenta assim:

$$ \begin{array}{|c|c|} \hline \times& 0 & 1 \\\hline 0 & 0 & 0\\\hline 1 & 0 & 1\\\hline \end{array}$$

A multiplicação em binário é efetuada de forma análoga à multiplicação decimal. Vejamos aqui alguns exemplos.

Exemplo 1: 101₂ x 11₂

$$ \begin{array}{r} 101 \\ \times \,\, 11\\\hline 101\\ 101\,\,\\\hline 1111 \end{array}$$

Exemplo 2: 110110₂x 110₂

$$ \begin{array}{r} 110110\\ \times \,\, 110\\\hline 000000\\ 110110\,\,\\ 110110\quad \\\hline 101000100 \end{array}$$

Divisão binária

A divisão em binário segue o mesmo princípio que a divisão decimal.

No seguinte exemplo descreve-se passo a passo o procedimento que você deve seguir.

Exemplo: 11101₂ / 10₂

Consideramos os primeiros dois dígitos do dividendo, e buscamos um múltiplo do divisor que seja próximo a 102. Neste caso o valor é 1.

Procedemos de maneira análoga ao passo anterior. O dígito seguinte (1), com o qual o novo dividendo é 112 e novamente o múltiplo de 102, próximo a 112 é o mesmo valor.

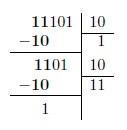
Finalmente repetindo o procedimento vemos que o resultado da divisão é 11102, ficando como resto 1.

Isso foi tudo o que você precisa saber para realizar operações com números binários, neste artigo apresentamos como realizar as operações de soma, subtração, multiplicação e divisão de números binários.

Se este artigo ou a calculadora de binários foram do seu agrado não deixe de compartilhar nas suas redes sociais, para que outras pessoas também possam aprender.

Agradecemos que se encontrar erros em nossas calculadoras, nos comunique usando o formulário de contato para que possamos solucioná-los o mais rápido possível.