Tabla de contenidos

Cómo usar la calculadora hexadecimal

Puedes realizar operaciones con números hexadecimales de forma fácil usando nuestraherramienta. Para ello solamente realiza lo siguiente:

Coloca en la primera casilla el primer número hexadecimal.
Selecciona la operación que deseas realizar (suma, resta, multiplicación o división).
Introduce el segundo número en hexadecimal.
Finalmente presiona “Calcular”.

Si deseas aprender a realizar manualmente las operaciones en hexadecimal, sigue leyendo este artículo.

Cómo convertir hexadecimal a decimal y viceversa

El sistema hexadecimal es un sistema de numeración posicional cuya base es el número 16.

Para expresar cada cifra se usan hasta 16 símbolos distintos. Estos símbolos están formados por los dígitos tradicionales del sistema decimal (0 a 9) y las seis primeras letras del alfabeto (A, B, C, D, E, F).

Para realizar la conversión es conveniente usar la siguiente tabla hexadecimal:

Decimal	Hexadecimal	Binario
0	0	0
1	1	1
2	2	10
3	3	11
4	4	100
5	5	101
6	6	110
7	7	111
8	8	1000
9	9	1001
10	A	1010
11	B	1011
12	C	1100
13	D	1101
14	E	1110
15	F	1111
16	10	10000
17	11	10001
18	12	10010
19	13	10011
20	14	10100
21	15	10101
22	16	10110
23	17	10111
24	18	11000
25	19	11001
26	1A	11010
27	1B	11011
28	1C	11100
29	1D	11101
30	1E	11110
31	1F	11111
32	20	100000
33	21	100001
34	22	100010
35	23	100011
36	24	100100
37	25	100101
38	26	100110
39	27	100111
40	28	101000
41	29	101001
42	2A	101010
43	2B	101011
44	2C	101100
45	2D	101101
46	2E	101110
47	2F	101111
48	30	110000
49	31	110001
50	32	110010
51	33	110011
52	34	110100
53	35	110101
54	36	110110
55	37	110111
56	38	111000
57	39	111001
58	3A	111010
59	3B	111011
60	3C	111100
61	3D	111101
62	3E	111110
63	3F	111111

Operaciones con números hexadecimales

Incremento

Cuando se incrementa en hexadecimal, cada posición de la cifras se incrementan una unidad desde 0 hasta la F. Cuando el dígito es F y se suma una unidad, el resultado es un cero y se incrementa la cifra de la posición siguiente.

Ejemplo de secuencia que comienza en 29:

29, 2A, 2B, 2C, 2D, 2E, 2F, 30, 31...

Ejemplo de secuencia que comienza en 5FB:

5FB, 5F9, 5FA, 5FB, 5FC, 5FD, 5FE, 5FF, 600, 601...

Suma hexadecimal

La suma hexadecimal sigue las mismas reglas de la suma decimal, teniendo en cuenta que el dígito de mayor valor es la F.

Puedes seguir este procedimiento:

Sumar los dos dígitos hexadecimales en decimal, insertando el equivalente hexadecimal para números mayores a 9
Si la suma es igual o menor a 15, esta puede expresarse como dígito hexadecimal.
Si la suma es mayor o igual a 16, se le resta 16 y se acarrea un uno (1) hacia el dígito de la siguiente posición.

Ejemplo 1: 2816 + 5416

$$ \begin{array}{r} 28 \\ + \,\, 54\\ \hline 7C \end{array}$$

Ejemplo 2: B716 + 2616

$$ \begin{array}{r} B7 \\ + \,\, 26\\\hline DD \end{array}$$

Ejemplo 3: 1FE16 + 95A16

$$ \begin{array}{r} 1FE \\ + \,\, 95A\\\hline B58 \end{array}$$

Resta hexadecimal

Para restar números hexadecimales se emplea el mismo método que para la resta binaria. Es decir, en vez de restar, se suma el complemento a 2 del número hexadecimal.

El sustraendo hexadecimal se complementa a 2 y luego se suma al minuendo. Si resulta acarreo se desprecia.

Ejemplo1: 5CA16 – 42C16

El sustraendo 42C se complementa a 2 así:

Hexadecimal	4	2	C
Binario	100	0010	1100
Complemento a 2	1011	1101	0100
Hex. Complemento a 2	B	D	4

Luego se efectúa la suma:

$$ \begin{array}{r} 5CA \\ + \,\, BD4\\\hline 119E \end{array}$$

Se desprecia el bit de acarreo y la resta da 19E.

Ejemplo2: 7F4B16 – 3ABC16

Hacemos el complemento a 2 de 3ABC:

Hexadecimal	3	A	B	C
Binario	0011	1010	1011	1100
Complemento a 2	1100	0101	0100	0100
Hex. Complemento a 2	C	5	4	4

Se realiza a suma:

$$ \begin{array}{r} 7F4B \\ + \,\, D654\\\hline 1459F \end{array}$$

Se desprecia el bit de acarreo y la resta da 459F.

Multiplicación hexadecimal

Para realizar la multiplicación es importante hacer uso de la siguiente tabla de multiplicación hexadecimal, similar a la que se usa en el caso decimal.

x	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F	10
1	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F	10
2	2	4	6	8	A	C	E	10	12	14	16	18	1A	1C	1E	20
3	3	6	9	C	F	12	15	18	1B	1E	21	24	27	2A	2D	30
4	4	8	C	10	14	18	1C	20	24	28	2C	30	34	38	3C	40
5	5	A	F	14	19	1E	23	28	2D	32	37	3C	41	46	4B	50
6	6	C	12	18	1E	24	2A	30	36	3C	42	48	4E	54	5A	60
7	7	E	15	1C	23	2A	31	38	3F	46	4D	54	5B	62	69	70
8	8	10	18	20	28	30	38	40	48	50	58	60	68	70	78	80
9	9	12	1B	24	2D	36	3F	48	51	5A	63	6C	75	7E	87	90
A	A	14	1E	28	32	3C	46	50	5A	64	6E	78	82	8C	96	A0
B	B	16	21	2C	37	42	4D	58	63	6E	79	84	8F	9A	A5	B0
C	C	18	24	30	3C	48	54	60	6C	78	84	90	9C	A8	B4	C0
D	D	1A	27	34	41	4E	5B	68	75	82	8F	9C	A9	B6	C3	D0
E	E	1C	2A	38	46	54	62	70	7E	8C	9A	A8	B6	C4	D2	E0
F	F	1E	2D	3C	4B	5A	69	78	87	96	A5	B4	C3	D2	E1	F0
10	10	20	30	40	50	60	70	80	90	A0	B0	C0	D0	E0	F0	100

Lo que se quiere es efectuar la multiplicación hexadecimal de forma análoga a la multiplicación decimal.

Ejemplo 1: F61016 x BE16

$$ \begin{array}{r} F610 \\ \times \,\, BE\\\hline D74E0\\ A92B0\quad \\\hline B69FE0 \end{array}$$

Ejemplo 2: 47A116 x DB16

$$ \begin{array}{r} 47A1 \\ \times \,\, DB\\\hline 313EB\\ 3A32D \quad \\\hline 3D46BB \end{array}$$

División hexadecimal

La división hexadecimal sigue el mismo principio que en otros sistemas numéricos. Veamos un ejemplo en donde realizaremos la división paso a paso.

Ejemplo: AE88716 / 3A16

Lo primero será realizar una tabla con los múltiplos de 3A, los cuales son:

1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
3A	74	AE	E8	122	15C	196	1D0	20A	244	27E	2B8	2F2	32C	366

Buscamos en la tabla primer múltiplo de 3A próximos a los dos primeros dígitos (AE). En este caso es 3.

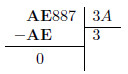
Hexadecimal division step 1

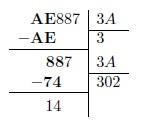
Procedemos de manera análoga al paso anterior. El dígito siguiente (8) es menor que 3A, razón por la cual agregamos un cero al cociente y realizamos la división al 88.

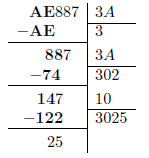
Buscamos un múltiplo de 3A próximo a 88. Revisando en la tabla apreciamos que este valor es 2, cuyo múltiplo es 74.

Hexadecimal division step 2

Finalmente, repitiendo el procedimiento, vemos que el resultado de la división es 3025, quedando como resto 25.

Hexadecimal division step 3

Esto ha sido todo lo que necesitas saber para realizar operaciones con números hexadecimales, en este artículo has aprendido paso a paso cómo efectuar la suma, resta, multiplicación y división de número en hexadecimal.

Si estás satisfecho/a con el artículo o con el calculador hexadecimal online, no dejes de compartirlos en tus redes sociales, para que otras personas también disfruten de esta comunidad.

x	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F	10
1	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F	10
2	2	4	6	8	A	C	E	10	12	14	16	18	1A	1C	1E	20
3	3	6	9	C	F	12	15	18	1B	1E	21	24	27	2A	2D	30
4	4	8	C	10	14	18	1C	20	24	28	2C	30	34	38	3C	40
5	5	A	F	14	19	1E	23	28	2D	32	37	3C	41	46	4B	50
6	6	C	12	18	1E	24	2A	30	36	3C	42	48	4E	54	5A	60
7	7	E	15	1C	23	2A	31	38	3F	46	4D	54	5B	62	69	70
8	8	10	18	20	28	30	38	40	48	50	58	60	68	70	78	80
9	9	12	1B	24	2D	36	3F	48	51	5A	63	6C	75	7E	87	90
A	A	14	1E	28	32	3C	46	50	5A	64	6E	78	82	8C	96	A0
B	B	16	21	2C	37	42	4D	58	63	6E	79	84	8F	9A	A5	B0
C	C	18	24	30	3C	48	54	60	6C	78	84	90	9C	A8	B4	C0
D	D	1A	27	34	41	4E	5B	68	75	82	8F	9C	A9	B6	C3	D0
E	E	1C	2A	38	46	54	62	70	7E	8C	9A	A8	B6	C4	D2	E0
F	F	1E	2D	3C	4B	5A	69	78	87	96	A5	B4	C3	D2	E1	F0
10	10	20	30	40	50	60	70	80	90	A0	B0	C0	D0	E0	F0	100

x	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F	10
1	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F	10
2	2	4	6	8	A	C	E	10	12	14	16	18	1A	1C	1E	20
3	3	6	9	C	F	12	15	18	1B	1E	21	24	27	2A	2D	30
4	4	8	C	10	14	18	1C	20	24	28	2C	30	34	38	3C	40
5	5	A	F	14	19	1E	23	28	2D	32	37	3C	41	46	4B	50
6	6	C	12	18	1E	24	2A	30	36	3C	42	48	4E	54	5A	60
7	7	E	15	1C	23	2A	31	38	3F	46	4D	54	5B	62	69	70
8	8	10	18	20	28	30	38	40	48	50	58	60	68	70	78	80
9	9	12	1B	24	2D	36	3F	48	51	5A	63	6C	75	7E	87	90
A	A	14	1E	28	32	3C	46	50	5A	64	6E	78	82	8C	96	A0
B	B	16	21	2C	37	42	4D	58	63	6E	79	84	8F	9A	A5	B0
C	C	18	24	30	3C	48	54	60	6C	78	84	90	9C	A8	B4	C0
D	D	1A	27	34	41	4E	5B	68	75	82	8F	9C	A9	B6	C3	D0
E	E	1C	2A	38	46	54	62	70	7E	8C	9A	A8	B6	C4	D2	E0
F	F	1E	2D	3C	4B	5A	69	78	87	96	A5	B4	C3	D2	E1	F0
10	10	20	30	40	50	60	70	80	90	A0	B0	C0	D0	E0	F0	100

Resultado