Cómo usar la calculadora binaria

Realiza operaciones con números binarios de forma fácil, rápida y de manera gratuita usando nuestra herramienta.

Para ello solamente realiza lo siguiente:

1. Coloca en la primera casilla el primer número binario.
2. Selecciona la operación que deseas realizar (suma, resta, multiplicación o división).
3. Introduce el segundo número en binario.
4. Presiona “Calcular”.

Si deseas aprender a realizar por tu cuenta las operaciones en binario de forma manual, entonces continúa leyendo este artículo.

Qué es el sistema de numeración binario

El sistema binario, o sistema numérico binario, es un sistema de numeración posicional con base 2.

A diferencia del sistema decimal (que tiene el 10 como base) las únicas cifras que componen los números binarios son 0 y 1, es por ello por lo que se hacen llamar números binarios.

Entre todos los sistemas de numeración, este es, con el permiso del sistema decimal, el que podrás encontrar más veces, porque la base de la informática toma este sistema como referencia.

Para indicar que un número ha sido escrito mediante el sistema binario se incluye el subíndice 2, que indica base 2 o binaria:

$$ (0100)_{2} $$

Aquí, al introducir el número 2 como base, estamos señalando que se debe leer: “cero uno cero cero”, es decir, se leerán las cifras individualmente y no se interpretará como si fuese el número “cien” del sistema decimal.

Cómo convertir del sistema binario al sistema decimal

Después de haber visto estas pequeñas indicaciones preliminares, vamos a explicar cómo podemos transformar un número escrito con base 2 a base 10 y viceversa.

Para convertir un número binario en uno decimal debemos realizar el procedimiento que se describe de forma ejemplificada a continuación:

$$(1101)_{2} \text{ a decimal}$$

Pasos a realizar:

1. Colocamos los dígitos del número binario separados en una tabla, un dígito por columna.
2. De derecha a izquierda se coloca debajo de cada dígito potencias de 2, comenzando con la potencia cero (2⁰).
3. Realizamos la multiplicación de cada dígito con la potencia correspondiente.
4. Finalmente se suma cada uno de los resultados de las multiplicaciones anteriores para así obtener el número decimal.

La tabla siguiente resume el procedimiento descrito anteriormente:

Cómo convertir del sistema decimal al sistema binario

Para pasar del sistema decimal a un número binario, deberás dividir dicho número sucesivas veces por dos, dividiendo, eso sí, el cociente de cada operación, hasta que el último resultado sea el número 0.

$$N = (cociente)(2)+resto$$

A continuación se realizará un ejemplo para entender más fácilmente el procedimiento:

$$(75)_{10} \text{ a binario}$$

Comenzamos realizando la división del número 76 entre 2, lo cual nos deja como cociente 36 y resto 1.

Luego repetimos la operación con el cociente de forma reiterada hasta que este sea igual a 0.

Aquí tienes el resultado del proceso:

Por lo tanto, podemos concluir que el número 76 expresado en binario seria 1001100, se leen de arriba abajo, es decir el resto de la división de 1/2, es el primer número que colocaremos de izquierda a derecha al expresar la cifra en código binario.

Operaciones con números binarios

Suma binaria

Sumar en binario lo podemos hacer fácilmente siguiendo la siguiente tabla:

$$ \begin{array}{|c|c|} \hline +& 0 & 1 \\\hline 0 & 0 & 1\\\hline 1 & 0 & 10\\\hline \end{array}$$

Puedes observar que 1₂+1₂=10₂, que es el equivalente a 2 en el sistema decimal.

Aquí tienes más ejemplos:

Ejemplo 1: 1011₂ + 010₂

$$ \begin{array}{r} 1011 \\ + \,\,010\\ \hline 1011 \end{array}$$

Ejemplo 2: 101011₂ + 100111₂

$$ \begin{array}{r} 101011 \\ + 100110\\ \hline 1010001 \end{array}$$

Resta binaria

La sustracción no es conmutativa y por lo tanto deben distinguirse los elementos que intervienen en la operación: minuendo y sustraendo. El minuendo es el elemento del cual se resta el sustraendo.

Para realizar la sustracción binaria se debe realizar lo que se conoce como complemento a dos.

Para calcular el complemento a dos de un número binario se procede de la siguiente manera:

Consideremos el número N=41 como ejemplo, cuya representación binaria es 41=101001₂ donde n=6 dígitos.

El complemento a dos de 41 viene dado por:

$$ 2^n-N = 2^6 – 41 = 23 =010111_{2} $$

De esta forma para calcular la resta de números binarios debemos primero calcular el complemento a dos del sustraendo y luego se efectúa la suma. Si existe acarreo se desprecia.

Ejemplo 1: 010111₂ – 000110₂

El sustraendo 000110 se complementa a dos.

$$ 000110 = 6 $$

$$ 2^6-6 = 58 = 0111010_2 $$

Ahora efectuamos la suma:

$$ \begin{array}{r} 010111 \\ + 111010\\ \hline 1010001 \end{array}$$

Despreciamos el bit de acarreo quedando así la resta finalmente así:

$$10001_{1}=17$$

Ejemplo 2: 010011₂ – 111100₂

Hacemos el complemento a 2 de 111100:

$$ 111100 = 60 $$

$$ 2^6 -60 = 4 = 000100_{2} $$

Ahora efectuamos la suma:

$$ \begin{array}{r} 010011 \\ + 000100\\ \hline 010111 \end{array}$$

De esta manera tenemos que el resultado de la operación es 23.

Multiplicación binaria

En la multiplicación los elementos se llaman multiplicando y multiplicador. Los elementos que intervienen en la operación se llaman factores.

La tabla para multiplicar binarios se presenta así:

$$ \begin{array}{|c|c|} \hline \times& 0 & 1 \\\hline 0 & 0 & 0\\\hline 1 & 0 & 1\\\hline \end{array}$$

La multiplicación en binario se efectúa de forma análoga a la multiplicación decimal. Veamos aquí algunos ejemplos.

Ejemplo 1: 101₂ x 11₂

$$ \begin{array}{r} 101 \\ \times \,\, 11\\\hline 101\\ 101\,\,\\\hline 1111 \end{array}$$

Ejemplo 2: 110110₂x 110₂

$$ \begin{array}{r} 110110\\ \times \,\, 110\\\hline 000000\\ 110110\,\,\\ 110110\quad \\\hline 101000100 \end{array}$$

División binaria

La división en binario sigue el mismo principio que la división decimal.

En el siguiente ejemplo se describe paso a paso el procedimiento que debes seguir.

Ejemplo: 11101₂ / 10₂

Consideramos los primeros dos dígitos del dividendo, y buscamos un múltiplo del divisor que sea próximo a 102. En este caso el valor ese valor es 1.

Procedemos de manera análoga al paso anterior. El dígito siguiente (1), con lo cual el nuevo dividendo es 112 y nuevamente el múltiplo de 102, próximo a 112 es el mismo valor.

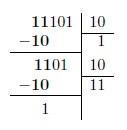
Finalmente repitiendo el procedimiento vemos que el resultado de la división es 11102, quedando como resto 1.

Esto ha sido todo lo que necesitas saber para realizar operaciones con números binarios, en este artículo te hemos presentado cómo realizar las operaciones de suma, resta, multiplicación y división de números binarios.

Si este artículo o la calculadora de binarios han sido de tu agrado no dejes de compartirlo en tus redes sociales, para que otras personas también puedan aprender.

Te agradecemos que consigues errores en nuestras calculadoras, nos lo comuniques usando el formulario de contacto para así poder solucionarlos lo más pronto posible.